ISO and teaching learning standards
Parallels between ISO and teaching/learning standards
Quite often we have people from a non-teacher background come into schools as a new teacher, or teachers leaving the teaching profession to move into a business or corporate career. In both cases our jobs have given us transferable skills. Further, the way that we analyze & improve our schools or businesses is much more similar than different.
Many companies use a group of standards called ISO to systematically look at and improve their company. Schools can benefit from the same ISO process. You can learn more about ISO here. A brief outline-
The International Organization for Standardization (ISO) is an independent, non-governmental organization composed of representatives from 170 nations. ISO has published over 25,000 international standards covering almost all aspects of technology and manufacturing. It creates international standards to make it much easier for companies to produce and sell products to other companies, governments, or individuals, across the world, e.g. manufactured products, food safety, transport, IT, agriculture, and healthcare.
Let’s look at official ISO ideas about how the system works and then see the parallels that can exist in a continually improving school system:
ISO standards are internationally agreed upon by experts. – iso. org
Learning standards are agreed upon by expert teachers in school districts across each state. Many states do so by drawing upon the Common Core and/or the Next Generation Science Standards (NGSS.)
ISO standards describe the best way of doing something. It could be about making a product, managing a process, delivering a service, or supplying materials – standards cover a huge range of activities. – iso. org
Common Core standards “define the rigorous skills and knowledge in English language arts and mathematics that need to be effectively taught and learned for all students to be ready to succeed academically in credit-bearing, college-entry courses and workforce training programs.” (Intro to Common Core State Standards for ELLs)
NGSS learning standards describe the best way of creating science-literate citizens; making science and engineering relevant to all students; and developing greater interest in science so that more students choose to major in science and technology in college.
ISO Standards are the distilled wisdom of people with expertise in their subject matter and who know the needs of the organizations they represent – people such as manufacturers, sellers, buyers, customers, trade associations, users, or regulators. – iso. org
Learning Standards are the distilled wisdom of people with expertise in teaching and who know the needs of both teachers and students.
ISO 9001 is a way for a company to think about and document precisely what they create, whether physical products or services. A company follows ISO 9001 standards to develop their own documents, procedures, and policies, customized to their needs.
Learning standards are a way for teachers to think about and document precisely what and how they are teaching, and how they assess student comprehension. Each school district or department develops their own documents, procedures, and policies customized to their needs.
ISO 9001 helps organizations of all sizes and sectors to improve their performance, meet customer expectations and demonstrate their commitment to quality.
Learning Standards are a way to help schools to improve their performance, meet community (teacher, parent and student) expectations, and demonstrate their commitment to helping each student reach their potential.
ISO requirements define how to establish, implement, maintain, and continually improve a quality management system (QMS).
Learning standards establish how admin and teachers can implement, maintain, and continually improve teaching in academic, vocational, music, art, and physical education classes.
Implementing ISO 9001 means your organization has put in place effective processes and trained staff to deliver flawless products or services time after time.
Implementing learning standards means that your school has put in place effective processes and trained staff to deliver the best possible educational experiences for the students of their local community.
Business benefits of ISO include:
Customer confidence: The standard ensures that organizations have robust quality control processes in place, leading to increased customer trust and satisfaction.
Effective complaint resolution: ISO 9001 offers guidelines for resolving customer complaints efficiently, contributing to timely and satisfactory problem-solving.
Process improvement: The standard helps identify and eliminate inefficiencies, reduce waste, streamline operations, and promote informed decision-making, resulting in cost savings and better outcomes.
Ongoing optimization: Regular audits and reviews encouraged by ISO 9001 enable organizations to continually refine their quality management systems, stay competitive, and achieve long-term success.
Community benefits of learning standards include:
Community confidence: The standard ensures that schools have robust quality control processes in place, leading to increased community trust and satisfaction.
Effective complaint resolution: Good school district policies offer ways to resolve complaints efficiently – taking seriously concerns of not only students but also teachers – contributing to timely and satisfactory problem-solving.
Process improvement: Good schools aim to identify and eliminate inefficiencies, streamline operations, and promote informed decision-making, resulting in cost savings to tax-payers and better outcomes for students.
Ongoing optimization: Regular audits – by teaching groups such as NEASC – enable schools to continually refine themselves and achieve long-term success.
How can we use the ISO process to help improve schools?
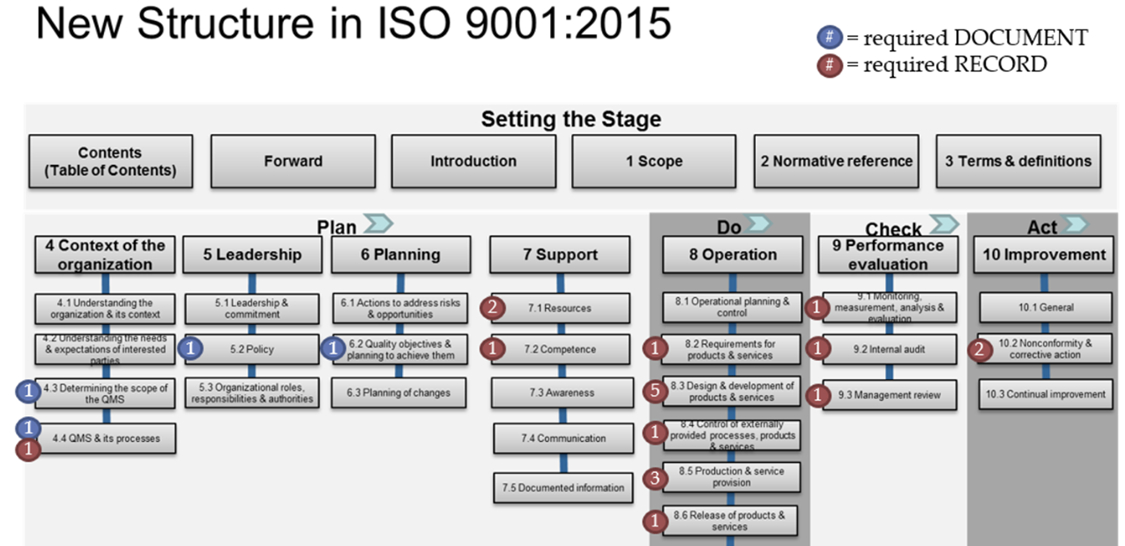
Many companies use ISO processes to systematically look at and improve their company. School districts and individual schools can benefit from the same ISO process. You can learn more about ISO here. This flowchart shows the structure of ISO 9001, and below we show it can be used in schools
Context of the organization
For a business – how is it organized? What is their QMS (quality management system?)
For a school – how is the school system organized? It usually looks something like this:
City or town school committee -> Superintendent -> School district teams and Principals -> Each individual school teacher and staff structure.
What kind of QMS do we find in schools?
Each school collects data on grades, attendance, safety, college or trade school or career acceptance, etc. They send this data to the appropriate district teams for discussion and analysis. This information should be made available to the school committee and general public.
Leadership
For a business, what are the leadership levels? They often look like:
President -> Vice president -> Department managers -> Employees within each department.
For a school, what are the leadership levels?
Principal -> assistant principals or deans ->teachers and paraprofessionals -> Students
Planning
For a business, what are the objectives and how does it achieve the objectives?
For a school, what are the objectives and how does it achieve the objectives? They may include:
* Promote a safe environment both for teachers and students
* Promote college and/or career readiness
* Develop young women and men into confident, self-directed, lifelong learners
* Develop young women and men to become productive members of their community
Support
For businesses – Resources, awareness, communication, documented information.
For schools –
Resources: Most classes have rooms with sufficient chairs and desks, bookshelves, supplies, manipulatives, lab equipment, textbooks (whether physical or digital;) computers/Chromebooks; school library, etc. Similarly, we can define what resources should be available for music, art, physical education, vocational education, special education, English Language Learners education, etc.
Awareness – There should be a structure for both teachers and students to have their concerns and needs heard by the administration.
Communication – Teachers communicate in regular department meetings and through email. The school has meetings for department heads for cross-curricular issues. There are whole-school meetings for all faculty/staff.
Documented information – This includes, but is not limited to, textbooks, teacher texts, worksheets, sample essays, quizzes, exams, labs, etc. (physical or digital,) and the district’s official learning standards (which may be local, state, national, or a combination thereof.)
Operations
For a business, we clearly define the production and delivery of products/services.
For a school we clearly define the creation/revision of pacing guides and lesson plans; and the implantation of these in the classroom, music room, art room, gym, etc.
Performance evaluation
For businesses: Is the product being made correctly? Monitoring, measurement, analysis, evaluation, internal audit. Management review.
For schools – Informal discussions, and asking questions, with students throughout the day. School quizzes and tests. State or national mandated standardized exams.
Improvement
For businesses – Identify any nonconformities and then decide what corrective actions would be helpful. A goal is continual improvement.
For schools – The parallel to nonconformities in schools could include –
– a student demonstrating that they didn’t (yet) learn certain facts; haven’t (yet) understood how individual facts were related in a greater whole; or haven’t (yet) mastered certain skills.
– a teacher demonstrating that they didn’t (yet) master how to create/revise pacing guides and lesson plans, or (yet) fully implement classroom management skills.
– an administrator demonstrating that they didn’t (yet) master how to help new or struggling teachers, how to help teachers who may feel targeted by students or parents, how to help students who have learning problems, how to help teachers or students who may be experiencing discrimination, etc.
and then decide what corrective actions would be helpful. The goal is continual improvement.
How to prepare for teaching AP Physics
So you have been assigned to teach a high school AP Physics class, congratulations! Teaching this or any AP high school science can be a fun, rewarding experience. There are ways to make it easier for new AP teachers coming into our schools. But if we don’t take such steps then we may set teachers up for failure. So here’s specific advice for those who have been asked to teach AP Physics for the first time:
* Have your school sign you up for an AP physics summer institute. Every high school should pay for this – and they should pay not only for the class, but also travel expenses, and room & board. The amount of money is peanuts compared to the school annual budget, and they know it. It is a one-time expense to create excellence for a program that impact many students for many years.
* Spend a few weeks talking with teachers who’ve taught AP physics before. They will be happy to share their notes with you. With their help, create a month-by-month pacing guide. As the year progresses try to stick with it so you get through all of the material.
* At the beginning of each unit/month, break your pacing guide down into a day-by-day pacing guide.
* Before the first day of school – get into the physics stockroom. Get into the online file/document storage, the bookshelves, and any storage cabinets that they have in the physics classrooms.
* Work with the teachers and science department head to find all the AP physics labs that AP physics students in your school have previously have been doing.
In theory, all of that should already be there for you, plug and play. But in reality many science department heads are overwhelmed, and have not made sure that this was done. In some schools when I walked in there was almost nothing organized for me. Many files were on somebody else’s hard drive or cloud drive, and those that were available were not always well organized or explained. Lab supplies were not always well organized or labeled.
* Plan ahead: You should try to run a couple of AP labs each month.
* Spend time – ideally, before the school year begins – going through the physics lab supply room. Find all items necessary to do the labs. For those items that you cannot find, work with your department head to write a purchase order to get what you need.
This can be a very doable job if there was good organization in the year before. There’s no reason for any school to not already have, for every new teacher walking in the door:
* A month by month, week by week AP pacing guide
* A good textbook or set of online resources that each lesson connects to
* Appropriate, well-labeled, and well-documented, AP physics labs.
* Clear lab write-ups for the teacher and for the students.
The challenges that we face are:
* Some people were disorganized. Their files may be in disarray.
* Some people create a detailed curriculum but take it with them and leave nothing for the new teacher. That shouldn’t be happening, we’re supposed to be a community where we all support and value each other.
* Some people lose parts/ lab supplies, don’t tell anyone, and don’t order replacement parts. That sets the next teacher up for frustration.
How we grow: One of the things I worked on over the years is showing my materials to teachers and students, and improving my process from their reactions. Sometimes what I wrote seems clear to me, yet someone will point out something ambiguous. This gives me an opportunity to rewrite and make things clearer.
Most problems for the next incoming AP science teachers go away as long as, in the previous year, the department head sits down with the science teachers and works things out ahead of time. Good intentions and a recognition that we are all part of a community leads to good organization and improvement of pedagogy. This benefits the entire community.
How do we plan a science class for topics left out by the NGSS?
What do we do when try to align a physics unit with NGSS – and NGSS doesn’t have anything on the topic?! For instance, NGSS seems to leave out: kinematics, vectors, parabolic motion, fluids, buoyancy, electrical circuits, rotational motion, geometric optics, and simple machines.
The official explanation is that NGSS standards are more about skills than content. That would be fair – except they do list specific content for so many other things. So what can we do?
We tie the physics topics that we teach into the NGSS in three ways:
(A) We teach students how to do problem solving in this unit. We address the NGSS problem solving and critical thinking skills.
(B ) Look into the NGSS Evidence statements. These offer many examples. Many of these evidence statements do specifically cover what we are looking for.
(C) We teach students how to do problem solving in this unit and cite the relevant, related Common Core Math standards that are addressed by this.
___________________________________
Thanks for visiting my website. We also have resources here for teachers of Astronomy, Biology, Chemistry, Earth Science, Physics, Diversity and Inclusion in STEM, and connections with reading, books, TV, and film. At this next link you can find all of my products at Teachers Pay Teachers, including free downloads – KaiserScience TpT resources
Which pedagogical strategy is best?
Anurag Katyal offers a great answer to this question!
Lectures work great, except when they don’t. Active Learning works great, except when it doesn’t. Just In Time teaching works great, except when it doesn’t. There’s no silver bullet. Context always matters.
Lectures work better for PhD students because they already have well defined boxes of knowledge in their head that they can file new information in. Younger students don’t have this and that’s why it doesn’t work nearly as well for them, yet it’s wrong to say it doesn’t work at all.
Active learning is fantastic for extroverted self-assured students who are up for the challenge. It doesn’t work as well for those who are painfully shy.
Just in time teaching works well for those who have some background already but need a reminder. You can’t do just in time remediation for factoring when a group of students does not know how to add signed numbers.
Context from day to day matters just as much – are you teaching at an independent school where a chipped nail is a crisis or at an underfunded public school in the inner city where kids don’t know where they will sleep that night.
Some techniques might work well in one school but not the other. You certainly can’t flip a classroom and have students watch YouTube videos ahead of class if they don’t have running water at home, let alone an internet connection. Well, you can try but it won’t go too well.
In my own classes, I find myself starting with inquiry as the highest ideal – and then going down the active learning scale based on the mood in the room on any given day. Sometimes, I have to go all the way to the bottom and lecture.
Sometimes, students pull me aside and say thanks for lecturing that day because xyz happened and they just would not have been a good group member. Other days, those students might be the first at the board.
Forget all the snazzy names and acronyms. Don’t let a pedagogy become your identity. Read the room. Adapt. Teach in a manner that will be best received that day. Remain flexible. Every 5 years, some new acronym comes out that’s the latest and greatest thing since sliced bread when all the students really wanted that day was a PBJ…
A master list of pedagodies/startegies:
Pedagogical strategies
Pedagogical theory
Bloom’s Taxonomy: Use and misuse
Bloom’s Taxonomy: Thinking well requires knowing facts (content and skills)
Levels – Levels of high school science classes
Honors – Why schools should offer Honors classes
Learning new information relies on having already existing knowledge.
Maslow’s hierarchy of needs – claims and reality
Students need to engage in internal mental reflection
Thinking well requires knowing facts
Tier I, II and III vocabulary
Learning styles and multiple intelligences
Reframing the Mind. Howard Gardner and the theory of multiple intelligences, By Daniel T. Willingham
Self esteem and students
Articles by cognitive scientist Daniel Willingham
Writing skills
One page notes/posters
Note taking skills
Good writing and avoiding plagiarism
How to write a physics lab report
Developing writing skills: Verb wheel
___________________
Thanks for visiting my website. We also have resources here for teachers of Astronomy, Biology, Chemistry, Earth Science, Physics, Diversity and Inclusion in STEM, and connections with reading, books, TV, and film. At this next link you can find all of my products at Teachers Pay Teachers, including free downloads – KaiserScience TpT resources
Spiral curriculum
Allan House writes
A spiral curriculum better matches with current understanding of how language is learned. Language can’t be broken down into discrete blocks which are independently masterable, revision is key to mastering items and skills and new vocabulary, learners will not truly learn a grammar point they are not ready for. They will only master a grammar form [or any topic] when they are at the right point in their learning. The repetition inherent in a spiral curriculum better allows for the above.
Learners come in with differing levels of language mastery, and jagged learning profiles. With a linear curriculum they may have missed some points which won’t be covered again. A spiral curriculum allows for revision of previously covered points, which also allows those with gaps to catch up in areas they are weaker in.
Robert Kaiser writes
Here is a visualization of linear learning. Each month, each year, we cover certain topics. In this lineal model we don’t come back to those topics again as time passes by. Rather, as time goes by we cover only new topics. The implicit assumptions here are:
* that everyone really learns – and learns well – the material the first time that they are exposed to it
* When learned encounter new material, they remember and understand the older material that this newer material depends on.
Yet good teachers understand that both of these assumptions are wrong.
For any topic in science (and also history, and ELA) students should instead cover content and skills in a spiraling fashion: They would start by being introduced to basic ideas in elementary school, at a level appropriate to their comprehension levels at the time.
Students must then be reintroduced to most of the same ideas in middle school, yet now at a deeper level. This time with more nuance, more facts. For some topics, with more mathematics. More sophisticated examples and more discussions. During this time we now include new topics that weren’t covered previously.
For those students taking high school classes, such as physics, chemistry, mathematics, they again should cover the same topics, but this time with more math, a richer set of examples, and of course newer material. Here is a visualization of how a spiral curriculum works:
Here is another such visualization.
As science teachers in high school we often have no control over elementary and middle school education, and often even little or no say in the overall curriculum of our own high schools. But if people would just listen to us teachers then they’d know we have a better way to teach science over time, this kind of teaching.
Thanks for visiting my website. We also have resources here for teachers of Astronomy, Biology, Chemistry, Earth Science, Physics, Diversity and Inclusion in STEM, and connections with reading, books, TV, and film. At this next link you can find all of my products at Teachers Pay Teachers, including free downloads – KaiserScience TpT resources
Wildlife rehabilitators in the greater Boston area
First some general advice from the Mass.gov wildlife website:
In almost all cases, it’s best to leave wildlife alone. If you determine that an animal needs intervention, you can contact a licensed wildlife rehabilitator for assistance using the map below. Young animals may seem helpless, but oftentimes they are neither abandoned nor orphaned and don’t require assistance. Animals taken out of the wild by well-intentioned people are often subjected to more stress and have a decreased chance of survival and ever having a normal life. Learn what to do if you find a wild animal that might be sick or injured.
Wild animals are protected by law. It is illegal to take an animal from the wild to care for or to attempt to keep as a pet. If you think that an animal may be in need of intervention, you can contact a licensed wildlife rehabilitator for assistance. Use the map of list below to find a rehabilitator near you. If using the map, click on an icon to get information about the rehabilitator.
Start out by contacting a rehabilitator to see if they can accept the animal. Next, get instructions about how to safely capture and transport the animal since rehabilitators are usually unable to pick up injured wildlife. Many rehabilitators specialize in treating certain types of animals, and not all rehabilitators may be able to accept every injured animal.
Suggestions
Cape Ann Wildlife, Inc. They specialize in birds. Essex, MA
http://caw2.org/
https://www.facebook.com/CapeAnnWildlifeInc/
Whalen’s Wildlife Rescue – We primarily rescue mammals and marsupials (opossums), but we do also intake reptiles and amphibians on a case-by-case basis.
https://whalenwildlife.org/home
New England Wildlife Center, Weymouth, MA near Braintree line.
https://www.facebook.com/NewEnglandWildlifeCenters/
New House Wildlife Rescue in Chelmsford MA
https://newhousewildliferescue.org/
https://www.facebook.com/NewhouseWildlifeRescue/
New ARC Northeast Wildlife Animal Rehabilitation Center:
We work out of our homes in Wilmington, Billerica, Chelmsford, Barre and Arlington, rehabilitating injured and orphaned wildlife brought to us by the general public or other animal rescue agencies (such as the Animal Rescue League of Boston or MSPCA). Injured animals are treated and orphaned animals are cared for until such a time as they are able to be released back into their natural habitat.
https://new-arc.org/index.html
Tufts Wildlife Clinic. Always call first – 508-839-7918
This does NOT accept healthy baby animals or those who are orphaned or abandoned.
https://vet.tufts.edu/tufts-wildlife-clinic
Cheryl Arena
Phone: 781-605-5565
Town: Malden
Species: Mammals (Cottontails, squirrels, chipmunks)
Daniel Proulx
Phone: 978-818-0016
Town: Marblehead
Species: Mammals (Text is best way to reach ASAP)
Jessica Reese – Salem Wildlife Rescue
Phone: 978-594-2652
Town: Salem
Species: Mammals (Limited intake in July, unavailable August 1-23. No raccoons, skunks, foxes, or bats; May be able to transport migratory birds)
Erin Gove
Phone: 609-316-2671
Town: Peabody
Species: Mammals (Text only
Jenna Medeiros
Phone: 978-717-3949
Town: Peabody
Species: Mammals (Squirrels only; Text only)
Maryanne Martin
Phone: 781-486-3826
Town: Wakefield
Species: Mammals (Rabbits only; Text message preferred)
Alesha Strycharz
Phone: 781-281-9560
Town: Stoneham
Species: Birds (Advice and limited triage/transfer. Texting preferred during the week)
Not authorized for migratory bird rehabilitation
Dan he is a rehabilitater in Marblehead
978-818-0016
Linda Amato
Phone: 617-605-2965
Town: Malden
Species: Mammals
Leah Desrochers
Phone: 603-553-2307
Town: Somerville
Species: Mammals, Birds, Reptiles (Triage/transfer and advice only)
Is it feasible and safe to colonize Mars?
Over the last decade many people working in space exploration have become much more skeptical about the possibility of human colonization of Mars, at least in the “near” term (which for these purposes covers the next century or two.)
Human exploration of Mars, of course, is a different thing altogether. There are many great reasons for humanity to send people to explore Mars. Some of these missions may involve people visiting the planet and living there for weeks or months. Soon after, some larger missions, centered around growing Mars bases, could have explorers choosing to spend a year or two on Mars before coming back to Earth.
So to be clear, this analysis is in full support of this growing exploration of our sister planet.
The concern here is about people who choose to engage in actual colonization – people who to Mars and have children there. What is life going to be like for humans born in the initially very small ,enclosed spaces on Mars? What will life be like for them in terms of psychological safety, physical safety? What will the effect be on future generations of people born on Mars?
Here are some problems with humans colonizing Mars
Almost no local resources
If there’s ever any breakdown in society, they have no energy producing resources to fall back on. There’s zero fossil fuels there. And as far as we know there’s almost zero sources for geothermal energy.
Wind energy
Using wind as energy could in principle work but the atmosphere of Mars is almost 99% less dense than Earth’s atmosphere, so Martian wind is very weak. It would take many huge wind generators to produce even a modest amount of electrical power.
Solar power
Solar power is possible on the surface of Mars. But since Mars is much further from the Sun than Eart is, the sunlight per square meter on the surface is much weaker. It would take vast areas of land to have an acceptable amount of energy for even small populations.
“Any self sustaining colonies will be totally dependent on power and the only really viable source is solar power. There is enough sunlight at Mars orbit, so it could be done. After all, the surface of Mars is as large as all the land on Earth, so there is room for extensive solar farms. This introduces two further problems, first making enough solar arrays would need a lot of resources that initially would have to be brought in to kick start it. But once past a certain point this could be done locally. The second is that Martian dust would regularly reduced efficiency requiring a crew of cleaners constantly keeping them dust free. Either automated or manually it would be a big task.”
“Massive orbital solar arrays beaming energy to the surface is another possibility; one could manufacture them on Phobos or Deimos. The initial operations would require fission or fusion to bootstrap, though. Mars’ geosynch is pretty close to the planet.”
Hydro-power and tidal-power
There’s no hydro-power on Mars because there are no streams.
There’s no tidal power because there’s no ocean. Even if there was an ocean, Mars has no large moon, so the ocean wouldn’t experience tidal forces. Mars will never have tides.
Nuclear fission power
For at least the near future – the next century – there’s almost no hope of mining significant amounts of uranium. It would be very difficult to create the infrastructure for mining and refining uranium, if it evebn exists there.
Worse, Mars has a significantly different geological history than Earth. It doesn’t have plate tectonics, at least not in any way like Earth. It has much less water erosion geological processes as well, due to the fact that its surface water dried up billions of years ago.
“On Earth those processes tend to move heavy metals towards the surface and concentrate them; on Mars (and on the Moon, and likely most asteroids as well) the concentrations will be scattered throughout the volume and hence much more resource intensive to mine.”
There’s another reason that Mars likely has far less nuclear material to mine:
“The Earth is a bit special. It had another planet strike it, mixing up the mantle, and redistributing the heavier elements. Mars had a more mundane formation. It cooled more slowly, concentrating the heavy elements deep in the crust. So lead, gold, platinum, thorium, uranium etc… will be rare.
As such, there may be no meaningful deposits of fissionable materials near the surface of Mars at all. Therefore, even nuclear power sources for Mars would have to be imported from Earth.
Geothermal power
“May be possible, Mars does have a near-surface temperature gradient that’s suitable (if not high potential) but it’d require drilling pretty deep, deeper than on Earth – although an advantage there is Mars has a very cold atmosphere and surface.”
Martian soil
Growing crops on Mars, in indoor domes with air and water, might be possible, but it could be very difficult. The soil is poisonous due to perchlorates and other molecules. People would need to develop economical ways to transform vast amounts of Martian soil into something safe for our crops to grow there.
Psychological health of humans raised indoors
There’s a lot of biological and psychological data on human health. We know that humans will not be mentally and physically healthy unless they have open space, blue skies, and a climate with natural spectrum sunlight much of the time.
Colonists living on Mars won’t have any of that unless, over many generations, we build extremely large, safe indoor biodomes. People living their lives on Mars would need grasslands, hiking trails, hills, places to climb, places to have picnics, places to play sports, etc.
People living on Mars would never be able to do something as simple as walk along the beach, sail a boat, or go on a hike in the woods.
So to ensure human health and happiness even at a minimum level, what would need to be done?
Society on Mars would need to dig out and safely enclose Superbowl stadium-sized areas, and not just one. A few dozen of them would be needed to provide the spacious environments necessary for psychological health. After all, the entire point of having a human colony on Mars is to have humans live and thrive on Mars – not to be prisoners for life in enclosed rooms and corridors.
Doing any of the massive digging necessary to do this would require tremendous amounts of power yet that’s precisely what we do not have a lot of on Mars.
I have seen the claim that a lack of sunlight, a lack of blue sky and the outdoors, would only be a first-generation problem. Some have held that people born on Mars would never know what they are missing. Firstly, there is no scientific evidence to support this position. Secondly, even hundredth generations of humans notice the “wrong” sunlight. It is known that increased rates of clinical depression are linked to people who live in regions with less sunlight even here on Earth. This is not surprising since our species evolved on the plains of Africa. Even human populations moving to a place on Earth like Siberia or Seattle, Washington, has caused an increase in psychological damage that isn’t being addressed.
Is there any possible way to minimize this? Above I mentioned the possibility that we could eventually dig out Superbowl stadium sized holes – these could have walls and ceilings covered with LEDs that simulate Earthly spring days, even with the appearance of clouds and sun.
Would humans evolve to become adapted to a Martian climate?
No. Evolution by natural selection would take hundreds of thousands of years to cause such changes. Consider, humans physiology has a genetic, biochemical 24 hour clock that has has a 28 day biochemical clock, and likely also a one year biochemical cycle. This is due to the fact that we humans evolved here on Earth, with a natural 24 hour day, 28.5 day lunar cycle, and 365 day year. Mars has no natural months – it has no major moon, and the Martian year is almost twice the length of the Earthly year. Even if we chose to allow natural selection to occur among humans on Mars – and we’ll get to that in a moment – it would take at least hundreds of thousands of years for this to create new genetic adaptations.
Many people, even some with otherwise good academic backgrounds, don’t understand the essential points of how evolution by natural selection works: In nature it works by most creatures dying, or living without ever finding a mate and passing their genes on to their offspring. Evolution happens because organisms in nature have no hospitals, medical care, or society to provide protection.
In contrast, once humans developed sophisticated families and tribes, likely at least 100,000 years ago, the rate of evolution suddenly dropped. Once intelligent beings developed the concept of family, love, and caring, instead of letting all the wounded or sick die, we took care of each other. So people who otherwise would have died – and tall their genes would be lost to the future gene pool – now had a better chance to live and pass on their genes.
Once humans developed more sophisticated medicine, more and people survived. Evolution slowed significantly. At least, not naturally. But humans could evolve to adapt to conditions on Mars – or on any other world – would be if people chose to allow some sort of natural selection to occur again, which could take tens of hundreds of thousands of years to produce significant effects. This would be horrible, and I know of no one who suggests any such thing.
Another way to dramatically increase the rate of evolution would be to use eugenics. No, not the horrific Nazi distortion of it, but rather just the basic idea: Have a society in which people make informed choices about who would be allowed to donate their own gametes for offspring. In principle this can be done by any group, at any time, through the use of sperm donors and IVF.
For instance, not everyone has the same biochemical clock. Human women, on average, have a 28.5 day menstrual cycle.
Men and women have – on average – a 24 hour daily cycle.
But that’s only an average, something we see when we look at large populations of people. For each individual person their cycles can be different from the mean. This provides an opportunity. Martians colonists could – if they freely choose to do so – look for people with the right biochemical cycles for Mars. Over time people could choose to use eggs and sperm from people with the right cycles in IVF procedures. So instead of taking millions of years, in just a few centuries a population could evolve that matches Martian daylight and yearly cycles.
People could also make other choices for genetics that would help people adapt to life on Mars, e.g. selecting for people who: have a higher resistance to radiation; have less SAD (seasonal affective disorder,) etc.
Evolution by natural selection
See our other articles on Astronomy and space exploration.
Thanks for visiting my website. We also have resources here for teachers of Astronomy, Biology, Chemistry, Earth Science, Physics, Diversity and Inclusion in STEM, and connections with reading, books, TV, and film. At this next link you can find all of my products at Teachers Pay Teachers, including free downloads – KaiserScience TpT resources
Soil profile Lego lab
First let’s learn about soil and its layers – Soil profiles
This image comes from Build a Layers of Soil Model by Sarah McClelland.
Clicking that links brings us to instructions for students to build their own realistic model of the Earth’s layers of soil. This can be adapted for use at any level of high school science.
Learning Standards
NGSS HS-ESS2-5. Plan and conduct an investigation of the properties of water and its effects on Earth materials and surface processes.
NGSS Science & Engineering Practices: Asking Questions and Defining Problems
Asking questions and defining problems in 9–12 builds on K–8 experiences and progresses to formulating, refining, and evaluating empirically testable questions and design problems using models and simulations.
-
Ask questions that arise from careful observation of phenomena, or unexpected results, to clarify and/or seek additional information.
Developing and Using Models – Predict and show relationships among variables between systems and their components in the natural and designed world(s)
-
Develop, revise, and/or use a model based on evidence to illustrate and/or predict the relationships between systems or between components of a system.
NGSS Appendix F – Science and Engineering Practices in the NGSS
Practice 3 Planning and Carrying Out Investigations
Planning and carrying out investigations in 9-12 builds on K-8 experiences and progresses to include investigations that provide evidence for and test conceptual, mathematical, physical, and empirical models…. Select appropriate tools to collect, record, analyze, and evaluate data.
Thanks for visiting my website. We also have resources here for teachers of Astronomy, Biology, Chemistry, Earth Science, Physics, Diversity and Inclusion in STEM, and connections with reading, books, TV, and film. At this next link you can find all of my products at Teachers Pay Teachers, including free downloads – KaiserScience TpT resources
Epithelial cell tissue box model
Students can build a realistic model of epithelial cells with a tissue box. Here’s an article on Skin – the integumentary System
Using a tissue box and some arts & crafts supplies students can build a fairly realistic model.
Similar labs
Skin Tissue Box Directions & Examples
Learning Standards
NGSS
HS-LS1-2 Develop and use a model to illustrate the hierarchical organization of interacting systems that provide specific functions within multicellular organisms
Disciplinary Core Ideas LS1.A: Structure and Function – Feedback mechanisms maintain a living system’s internal conditions within certain limits and mediate behaviors, allowing it to remain alive and functional even as external conditions change within some range. Feedback mechanisms can encourage (through positive feedback) or discourage (negative feedback) what is going on inside the living system
NGSS Evidence Standards: Observable features of the student performance by the end of the course:
1 – Components of the model – Students develop a model in which they identify and describe the relevant parts (e.g., organ system, organs, and their component tissues) and processes (e.g., transport of fluids, motion) of body systems in multicellular organisms
2 – Relationships – In the model, students describe the relationships between components
3. Connections – (a) Students use the model to illustrate how the interaction between systems provides specific functions in multicellular organisms, and (b) Students make a distinction between the accuracy of the model and actual body systems and functions it represents.
Thanks for visiting my website. We also have resources here for teachers of Astronomy, Biology, Chemistry, Earth Science, Physics, Diversity and Inclusion in STEM, and connections with reading, books, TV, and film. At this next link you can find all of my products at Teachers Pay Teachers, including free downloads – KaiserScience TpT resources